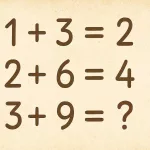L’énigme des équations cachées : quand la logique devient un jeu d’ombre et de lumière

À première vue, ces équations semblent n’être qu’un simple exercice d’algèbre. Pourtant, derrière leur apparente simplicité se cache une leçon bien plus profonde que la résolution d’inconnues. Ce n’est pas seulement une question de chiffres, mais une invitation à décrypter l’invisible, à percevoir les liens là où d’autres ne voient que des symboles.

Pourquoi ce genre de défi nous intrigue-t-il tant ?

Parce qu’il nous rappelle que les réponses les plus élégantes ne sont pas toujours celles qu’on attend. Les esprits brillants — qu’ils soient mathématiciens, stratèges ou rêveurs — savent une chose : la clé ne réside pas toujours dans ce qui est écrit, mais dans ce qui est sous-entendu.

Comme le disait le philosophe Ludwig Wittgenstein : « Les limites de mon langage sont les limites de mon monde. » Autrement dit, si vous ne voyez qu’une équation, vous passerez à côté de l’essentiel.

Imaginez : vous êtes face à un problème, au travail, dans une discussion, ou même dans une décision personnelle. Les données sont là, claires, mais quelque chose cloche. Vous tournez en rond, jusqu’à ce qu’un déclic se produise… 

Et si la solution n’était pas dans les nombres eux-mêmes, mais dans la façon dont ils dansent ensemble ?

Cette énigme est une métaphore : parfois, il faut écouter le silence entre les notes pour comprendre la mélodie.

À vous de jouer ! Lâchez les calculs mécaniques, laissez votre intuition guider votre regard. 

Et si la solution était déjà là, cachée dans l’harmonie des signes ? 

Quand vous aurez trouvé, vous aurez découvert bien plus qu’un résultat : une nouvelle façon de voir les problèmes, où la logique et la créativité ne font qu’un.

Alors, que vaut P × Q ?

La réponse est là, tapie dans l’équilibre entre ce qui est donné et ce qui reste à deviner. Un indice ? Et si le vrai mystère n’était pas de chercher P ou Q séparément, mais de les voir comme les deux faces d’une même pièce ? 

Comme un dialogue où chaque réplique éclaire l’autre…

Une fable pour éclairer l’énigme : Un élève, frustré, demanda un jour à son maître : 

« Comment résoudre ce qui semble insoluble ? » Le maître prit deux pierres, l’une légère, l’autre lourde, et les posa sur une balance. « Vois-tu ? dit-il. Si tu ne regardes que le poids de chaque pierre, tu resteras bloqué. Mais si tu observes comment elles s’équilibrent, tu comprendras leur secret. » 

L’élève médita, puis sourit : la réponse n’était pas dans les pierres, mais dans l’espace qui les unissait.

Voici la solution que nous avons trouvée :

1. Système :

P + Q = 10, P ÷ Q = 4

2. Transformer la division :

P = 4Q

3. Substituer dans P + Q = 10 :

4Q + Q = 10 → 5Q = 10 → Q = 2

4. Trouver P :

P = 4 × 2 = 8

5. Calculer le produit :

P × Q = 8 × 2 = 16

Réponse finale : 16

Alors si vous avez apprécié ce test, n’oubliez pas de relever de faire d’autres tests ou d’autres défis de notre section de lectures recommandées en cliquant ici.